This post provides a brief overview of the Computational Fluid Dynamics (CFD) solver used during my thesis, which is dubbed EVA and developed by Citation: Eijk & Wellens (2022) Eijk, M. & Wellens, P. (2022). Two-phase free-surface flow interaction with moving bodies with a consistent, momentum preserving method. Journal of Computational Physics. . EVA is able to solve two-phase (in-)compressible fluid flows and uses consistent two-way fluid-structure interactions (FSI), where applying this to moving bodies together with a Volume-of-Fluid (VoF) cut-cell method on a staggered arrangement of variables is a novelty of EVA (Citation: Eijk & Wellens, 2022 Eijk, M. & Wellens, P. (2022). Two-phase free-surface flow interaction with moving bodies with a consistent, momentum preserving method. Journal of Computational Physics. ).

The goal of this post is to provide sufficient insight into the CFD solver used in this work, such that there is some understanding of the simulation process and the related challenges encountered in this thesis. This post is not meant to provide details on the level of complete reproducibility of the CFD code. A more detailed and complete description of EVA is given by Citation: Eijk & Wellens (2022) Eijk, M. & Wellens, P. (2022). Two-phase free-surface flow interaction with moving bodies with a consistent, momentum preserving method. Journal of Computational Physics. .

This post will consider some core concepts of EVA in the following order:

• Governing equations.
• Cell-labelling, interface reconstruction, and cut-cell definition.
• Transport of fluid and bodies.
• Solving method.

Governing Equations

EVA solves the discrete 2D Navier-Stokes equations for mass and momentum conservation in partial differential conservative form, see $\cref{eqn:continuity_equation}{1}$ and $\cref{eqn:momentum_equation}{2}$. $\cref{eqn:continuity_equation}{1}$ is regularly referred to as the continuity equation. EVA employs the one-fluid formulation with a single velocity field, a single pressure field and a thereof resulting fluid mixture density, thereby only requiring one set of equations for all the fluids combined.

\begin{equation}\label{eqn:continuity_equation} \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \mathbf{u})=0 \end{equation} \begin{equation}\label{eqn:momentum_equation} \frac{\partial(\rho \mathbf{u})}{\partial t}+\nabla \cdot(\rho \mathbf{u}\otimes\mathbf{u})+\nabla p-\nabla \cdot\left(\mu\left(\nabla \mathbf{u}+\nabla \mathbf{u}^{T}\right)-\frac{2}{3} \mu \nabla \cdot \mathbf{u}\right)-\rho \mathbf{f}=0 \end{equation}

Here $\mathbf{u} = \left(u,v\right)$ $[m/s]$ is the fluid velocity vector, $p$ the fluid pressure, $\nabla = \left(\frac{\partial}{\partial x},\frac{\partial}{\partial y}\right)$ is the gradient operator, $\mu$ $[Pa\cdot s]$ the dynamic viscosity of the fluid (mixture), and $\mathbf{f}$ $[kg/ m^2 s^2]$ represents the body forces comprised of the gravitational acceleration and capillary stresses. Lastly, $\rho$ $[kg/m^3]$ is the fluid mixture density, of which Citation: Eijk & Wellens (2022) Eijk, M. & Wellens, P. (2022). Two-phase free-surface flow interaction with moving bodies with a consistent, momentum preserving method. Journal of Computational Physics. provide a detailed description.

To achieve consistent mass-momentum transport at the interfaces, EVA additionally solves a temporary auxiliary continuity equation (Citation: Zuzio, Orazzo & al., 2020 Zuzio, D., Orazzo, A., Estivalèzes, J. & Lagrange, I. (2020). A new efficient momentum preserving Level-Set/VOF method for high density and momentum ratio incompressible two-phase flows. Journal of Computational Physics, 410. https://doi.org/10.1016/j.jcp.2020.109342 ).

Because we are involved with the transport of two phases the transport equation $\cref{eqn:VoF_transport}{3}$ is solved. Here, the one-fluid velocity field results in the assumption of no-slip between the fluids and therefore the fluid velocity can be used instead of the interface velocity.

\begin{equation}\label{eqn:VoF_transport} \frac{\partial F}{\partial t}+\mathbf{u} \cdot \nabla F=0 \end{equation} Here, $F(x,t) = 0$ provides the location of the interface in space and time. To solve $\cref{eqn:VoF_transport}{3}$, EVA employs the Volume of Fluid (VoF) method (Citation: Hirt & Nichols, 1981 Hirt, C. & Nichols, B. (1981). Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics, 39(1). 201–225. https://doi.org/10.1016/0021-9991(81)90145-5 ), for which the continuous colour function $F$ is replaced by a discrete volume fraction $C$ with a value between 0 and 1; now indicating the ratio of the cell volume occupied by the corresponding phase. The discretized $\cref{eqn:VoF_transport}{3}$ is then solved using an advection scheme.

The rigid body is displaced explicitly using:

\begin{equation} \frac{\partial \mathbf{x}_b}{\partial t}=\mathbf{u}_b \end{equation}

Here, the body velocity $\mathbf{u}_b$ is found through Newton’s second law, using the known constant body mass $m_b$:

\begin{equation} m_b \frac{\partial \mathbf{u}_b}{\partial t}=\mathbf{F}_b \end{equation}

$\mathbf{F}_b$ is composed of the gravitational force and the normal pressures of the fluid integrated over the body boundary surface. Viscous stresses are neglected in the calculation of the body forces since EVA focuses on the dynamics of impacts: an event within a short-time period during which viscous effects such as boundary layers cannot develop.

Cell-labelling, interface reconstruction, and cut-cell definition

The one-fluid formulation that EVA uses relies on the accurate identification and definition of the (cells on the) interface between the different phases to perform correct fluid calculations. This section introduces the steps, definitions and notations needed to achieve this.

Roughly, the procedure is as follows:

• Cell labelling: Based on a known (updated) Volume of Fluid fraction field $C$, each cell is given a label defining its composition and relation to neighbouring cells.
• Interface reconstruction: Using the cell labelling and the volume fraction field, the fluid and material interfaces are geometrically reconstructed.
• Cut-cell definition: The reconstructed interfaces are then used to define the cut-cell geometries, which are eventually used to correctly solve the momentum equations.

Cell labelling

Cell labelling is used by EVA to distinguish between different possible scenarios and configurations of a (cut-)cell, indicating what computational routines should be used during the fluid calculations and interface reconstruction.

The cell labelling is explained by means of Fig. 1, while I refer to Citation: Eijk & Wellens (2022) Eijk, M. & Wellens, P. (2022). Two-phase free-surface flow interaction with moving bodies with a consistent, momentum preserving method. Journal of Computational Physics. for a complete description of the cell labelling process.

Interface reconstruction

The interface is being approximated by a line (or a plane in three dimensions) using the Piecewise-Linear Interface Calculation (PLIC) method (Citation: Youngs, 1984 Youngs, D. (1984). An interface tracking method for a 3D Eulerian Hydrodynamics code. Awre(Technical Report 44/92/35). ; Citation: Düz, Borsboom & al., 2016 Düz, B., Borsboom, M., Veldman, A., Wellens, P. & Huijsmans, R. (2016). Efficient and accurate PLIC-VOF techniques for numerical simulations of free surface water waves. 9th International Conference on Computational Fluid Dynamics, ICCFD 2016 - Proceedings. ). For each 2D cell the interface is approximated using:

\begin{equation} \boldsymbol{m\cdot x} = m_xx + m_yy = \alpha \end{equation}

Here $\boldsymbol{m}$ is the local surface normal, $\boldsymbol{x}$ is the position vector of a point on the interface and $\alpha$ is the plane constant placing the line at a distance from the origin of the cell. $\boldsymbol{m}$ is calculated using the neighbouring volume fraction field and its gradients, where Citation: Düz, Borsboom & al. (2016) Düz, B., Borsboom, M., Veldman, A., Wellens, P. & Huijsmans, R. (2016). Efficient and accurate PLIC-VOF techniques for numerical simulations of free surface water waves. 9th International Conference on Computational Fluid Dynamics, ICCFD 2016 - Proceedings. considers various methods to do so and EVA makes use of the cell labelling. In 2D, the plane constant $\alpha$ is analytically calculated by matching the volume resulting from the combination between the surface normal $m$ and the plane constant $\alpha$ with the required fraction volume $C_f$.

During the interface reconstruction, EVA is able to use the appropriate calculations by using the cell-labelling, where Citation: Eijk & Wellens (2022) Eijk, M. & Wellens, P. (2022). Two-phase free-surface flow interaction with moving bodies with a consistent, momentum preserving method. Journal of Computational Physics. show that the introduced C-labelling provides significant improvements.

Cut-cell definition

Given a known reconstructed fluid interface, this section defines the thereof resulting cut-cell geometry (Citation: Kleefsman, Fekken & al., 2005 Kleefsman, K., Fekken, G., Veldman, A., Iwanowski, B. & Buchner, B. (2005). A Volume-of-Fluid based simulation method for wave impact problems. Journal of Computational Physics, 206(1). 363–393. https://doi.org/10.1016/j.jcp.2004.12.007 ; Citation: Fekken, 2004 Fekken, G. (2004). Numerical Simulation of Free-Surface Flow with Moving Rigid Bodies  (PhD thesis). ). The material interface cuts through a regular fixed Cartesian grid-cell and thus divides the cell into different regions, which is why such a cell is called a cut-cell. The cut-cell geometry provides the definitions and control volumes that are important for correct momentum calculations at the body interface, seeing that the body is rigid and should not partake in the fluid calculations.

Fig. 2 visually provides the full cut-cell definition using two situations:

• Subfigures (a), (b): Air is cut by the body (dark grey)
• Subfigure (c): $\hspace{13pt}$ Additionally, the air is cut by fluid (light grey)

In the first scenario we are involved with the body volume fraction $C_{b,i,j}$ while in the second scenario we are additionally involved with the fluid volume fraction $C_{f,i,j}$. These volume fractions describe the portion of the cell volume ($=\delta x_i \delta x_j$ in a 2D structured grid) that is occupied by the corresponding phase.

Fig. 2a portrays the body apertures $a_b$, which defines the portion of each of the cell’s edges that is open to flow between cells and defines the size of the control volume. $\delta x_i$ and $\delta y_j$ are respectively the horizontal and vertical size of grid cell (i,j).

In this section, I do not consider the added complexity introduced by the methodology of Citation: Zuzio, Orazzo & al. (2020) Zuzio, D., Orazzo, A., Estivalèzes, J. & Lagrange, I. (2020). A new efficient momentum preserving Level-Set/VOF method for high density and momentum ratio incompressible two-phase flows. Journal of Computational Physics, 410. https://doi.org/10.1016/j.jcp.2020.109342 , used by EVA to simultaneously be momentum- and mass-conserving. This methodology defines additional control volumes that leave us with a more complicated sub-grid cut-cell formulation. For an account on this matter, I refer to Citation: Zuzio, Orazzo & al. (2020) Zuzio, D., Orazzo, A., Estivalèzes, J. & Lagrange, I. (2020). A new efficient momentum preserving Level-Set/VOF method for high density and momentum ratio incompressible two-phase flows. Journal of Computational Physics, 410. https://doi.org/10.1016/j.jcp.2020.109342 ; Citation: Eijk & Wellens (2022) Eijk, M. & Wellens, P. (2022). Two-phase free-surface flow interaction with moving bodies with a consistent, momentum preserving method. Journal of Computational Physics. .

Transport of the fluids and body

This section summarizes the methods that EVA uses for solving the transport equation $\cref{eqn:VoF_transport}{3}$ for both the fluid- and body volume fraction fields using a known velocity field $\boldsymbol{u}$ and the interface reconstruction procedure.

First, a definition of flux, whereafter the various advection or fluxing schemes of EVA are discussed. Lastly, I discuss the controller that ensures numerical stability during fluxing.

Flux definition

Flux is the transport or flow of a quantity through a surface. In the case of EVA, that surface is the side of a cell defined in the structured grid as a 2D line with unit depth. The transported quantity is a material or fluid represented by the volume fractions $C_b$ or $C_f$.

For an uncut fluid cell in a structured grid, the (average) fluid flow over that side is represented using a single velocity normal to the surface. The horizontal flux over the right side of cell (i,j) is then:

\begin{equation}\label{eqn:flux} \delta C_{f,i+\frac{1}{2},j} = u_{i+\frac{1}{2},j}\cdot \delta t \end{equation}

In the case of a cut-cell the flux calculation is more complicated due to the presence of interfaces. Fig. 3 depicts the scenario of a cut-cell with both a body and fluid interface, where we are again interested in the flux of the fluid fraction over the right cell boundary. The amount of fluxed fluid is limited by both the body-fluid interface and the air-fluid interface.

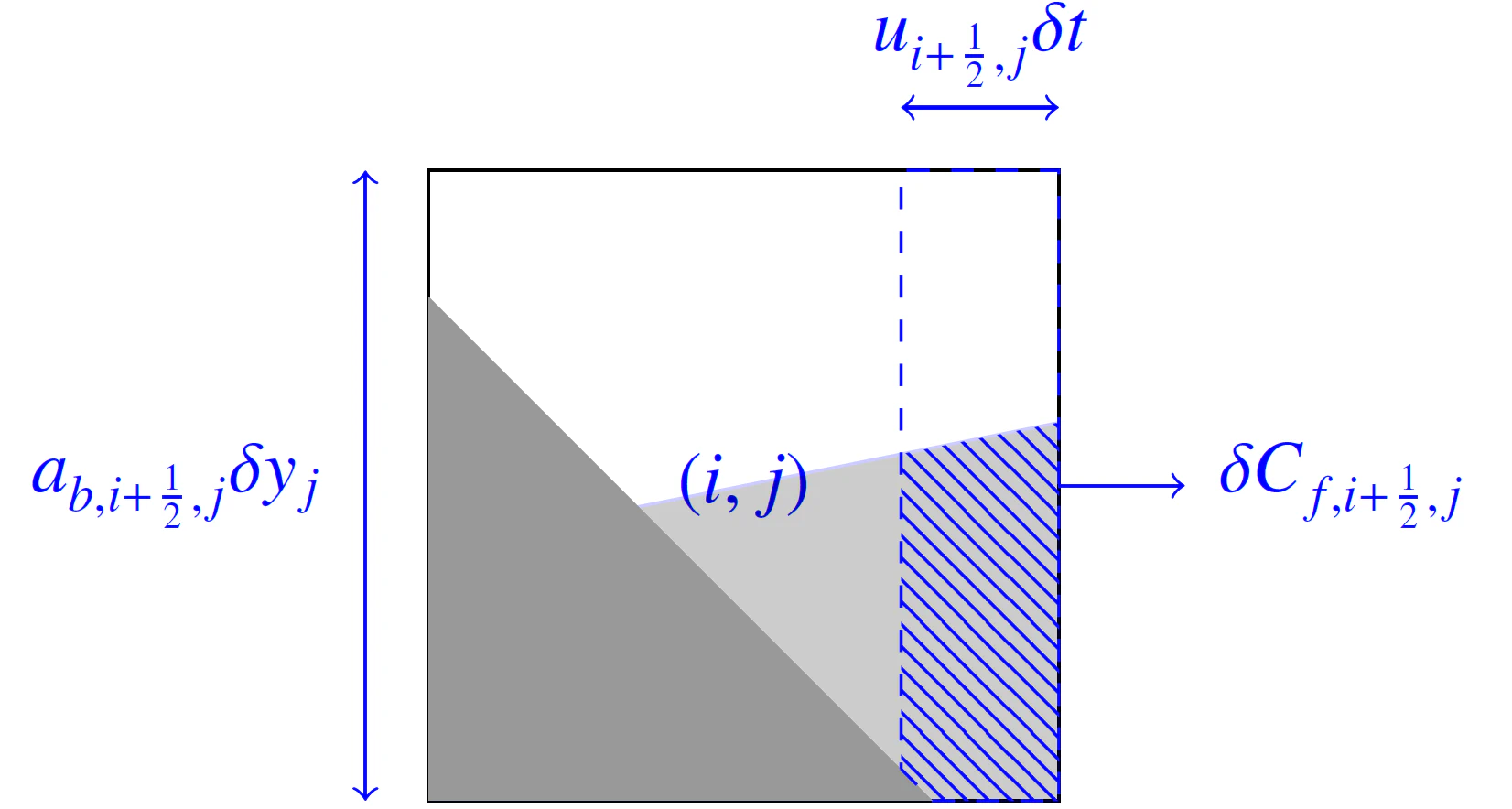
Fluxing schemes

This section summarizes the methods that EVA uses for solving the discretized transport equation $\cref{eqn:VoF_transport}{3}$ for both the fluid- and body volume fraction fields. Citation: Düz, Borsboom & al. (2016) Düz, B., Borsboom, M., Veldman, A., Wellens, P. & Huijsmans, R. (2016). Efficient and accurate PLIC-VOF techniques for numerical simulations of free surface water waves. 9th International Conference on Computational Fluid Dynamics, ICCFD 2016 - Proceedings. provide an elaborate account of these methods and identifies two approaches: using an unsplit advection scheme or an operator-split advection scheme.

In the unsplit advection method, hereafter referred to as UNSPLIT, the body fraction $C$ and corresponding body interface is propagated within a single update $C^n \rightarrow C^{n+1}$ according to a known velocity field. Although this only requires one fluid interface reconstruction step and thus is cheap, we encounter problems for multi-directional body velocities. For instance, with 2D diagonal body movement the same interfacial volume can be doubly advected while none of the corresponding body fraction is actually displaced diagonally, but only vertically and horizontally in an isolated fashion. This process is called overlapping (Citation: Comminal, Spangenberg & al., 2015 Comminal, R., Spangenberg, J. & Hattel, J. (2015). Cellwise conservative unsplit advection for the volume of fluid method. Journal of Computational Physics, 283. 582–608. https://doi.org/10.1016/j.jcp.2014.12.003 ) and results in mass loss. Similarly non-overlapping creates gaps leading to diffusion. Thereby, UNSPLIT is prone to mass conservation problems and does not inherently preserve the body shape and interface.

On the other hand, operator-split advection schemes flux the body volumes sequentially and separately per direction. As such they are inherently mass conserving and able to advect volumes to diagonally neighbouring cells within a single timestep.

EVA and (Citation: Düz, Borsboom & al., 2016 Düz, B., Borsboom, M., Veldman, A., Wellens, P. & Huijsmans, R. (2016). Efficient and accurate PLIC-VOF techniques for numerical simulations of free surface water waves. 9th International Conference on Computational Fluid Dynamics, ICCFD 2016 - Proceedings. ) consider two operator-split advection schemes:

• MACHO: Multidimensional Advective-Conservative Hybrid Operator
• COSMIC: Conservative Operator Splitting for Multidimensions with Inherent Constancy

COSMIC considers each sequential update ordering permutation at once, while MACHO only considers one such permutation per timestep. Instead, MACHO alternates between these permutations during subsequent timesteps to reduce directional bias. Therefore, COSMIC is in principle more accurate and reliable but much more expensive, requiring additional interface reconstructions for each permutation.

The 2D MACHO scheme is formulated:

\begin{equation}\label{eqn:MACHO_permutation} \begin{aligned} C^{*} &= C^{n} - \Delta t \frac{\partial u C^{n}}{\partial x} + \Delta t C^{n} \frac{\partial u}{\partial x}, \\ C^{n+1} &= C^{n} - \Delta t \left(\frac{\partial u C^{n}}{\partial x} + \frac{\partial v C^{*}}{\partial y}\right), \end{aligned} \end{equation}

To clarify, in 2D MACHO alternates between $\cref{eqn:MACHO_permutation}{8}$ and:

\begin{equation} \begin{aligned} C^{*} &=C^{n}-\Delta t \frac{\partial v C^{n}}{\partial y}+\Delta t C^{n} \frac{\partial v}{\partial y}, \\ C^{n+1} &=C^{n}-\Delta t\left(\frac{\partial u C^{*}}{\partial x}+\frac{\partial v C^{n}}{\partial y}\right), \end{aligned} \end{equation}

The 2D COSMIC scheme is formulated: \begin{equation} \begin{aligned} C^{X} &=C^{n}-\Delta t \frac{\partial u C^{n}}{\partial x}+\Delta t C^{n} \frac{\partial u}{\partial x} \\ C^{Y} &=C^{n}-\Delta t \frac{\partial v C^{n}}{\partial y}+\Delta t C^{n} \frac{\partial v}{\partial y}, \\ C^{n+1} &=C^{n}-\Delta t\left[\frac{\partial}{\partial x}\left(u \frac{C^{n}+C^{Y}}{2}\right)+\frac{\partial}{\partial y}\left(v \frac{C^{n}+C^{X}}{2}\right)\right] \end{aligned} \end{equation}

In 2D, UNSPLIT requires one interface reconstruction (once per time-step update), MACHO requires two, and COSMIC requires three interface reconstructions. In 3D however, UNSPLIT still requires one interface reconstruction, MACHO requires three, and COSMIC requires a significant amount of 10 interface reconstructions. For the full definitions of MACHO and COSMIC in 3D, I refer to (Citation: Düz, Borsboom & al., 2016 Düz, B., Borsboom, M., Veldman, A., Wellens, P. & Huijsmans, R. (2016). Efficient and accurate PLIC-VOF techniques for numerical simulations of free surface water waves. 9th International Conference on Computational Fluid Dynamics, ICCFD 2016 - Proceedings. ).

CFL controller

To maintain numerical stability during fluxing, EVA employs a time-step controller based on the Courant–Friedrichs–Lewy (CFL) condition (Citation: Courant, Friedrichs & al., 1928 Courant, R., Friedrichs, K. & Lewy, H. (1928). On the Partial Difference Equations of Mathematical Physics. Mathematische Annalen, 138(2). 179–202. https://doi.org/10.1007/BF01342943 ). The CFL controller prevents fluxing more fluid than there is present inside a cell. It decreases the time-step size $\Delta t$ if the flux is too high anywhere in the grid, and similarly increases it when fluxes can be higher without violating the condition. This ensures that at any time during the simulation we use the appropriate timestep size, thereby balancing numerical efficiency and stability. The CFL condition in 1D is defined as: \begin{equation} \frac{u \Delta t}{\partial x} \overset{?}{<=} CFL_{max} \end{equation}

Since EVA operates in a structured grid we choose to apply this rule per dimension. The dimensionless number $CFL_{max}$ is called the Courant number. For $CFL_{max} = 1$ (with the valid range of $C_{max}$ defined by $0<CFL_{max} <= 1$), the condition entails that the displacement of some piece of fluid cannot be larger than a grid cell’s size a given dimension. In other words, we should not be able to ‘skip’ an entire grid cell during a timestep, which would lead to numerical instability.

Generally, a $CFL_{max}$ lower than 1 provides more numerical stability and is often required. Of course, this potentially comes at the cost of smaller used time-steps and therefore higher simulation times.

Solving method

This section considers how EVA solves the Navier-Stokes equations ($\cref{eqn:continuity_equation}{1}$ and $\cref{eqn:momentum_equation}{2}$). In basis, to solve the discretized Navier-Stokes equations EVA employs the so-called \textit{pressure correction} projection approach (Citation: Eijk & Wellens, 2022 Eijk, M. & Wellens, P. (2022). Two-phase free-surface flow interaction with moving bodies with a consistent, momentum preserving method. Journal of Computational Physics. ). EVA does so by using a second-order upwind space integration scheme and the Adam-Bashforth time integration scheme (Citation: Eijk & Wellens, 2022 Eijk, M. & Wellens, P. (2022). Two-phase free-surface flow interaction with moving bodies with a consistent, momentum preserving method. Journal of Computational Physics. ). The complete solving method of EVA includes additional steps to calculate effective densities at the VoF interface to enable compressible fluid calculations. These density calculations are in turn related to the method of Citation: Zuzio, Orazzo & al. (2020) Zuzio, D., Orazzo, A., Estivalèzes, J. & Lagrange, I. (2020). A new efficient momentum preserving Level-Set/VOF method for high density and momentum ratio incompressible two-phase flows. Journal of Computational Physics, 410. https://doi.org/10.1016/j.jcp.2020.109342 for consistent calculations at the fluid interfaces. Since these topics are considered too in-depth and non-relevant for the goals of this work, I refer to Citation: Bockstael (2021) Bockstael, M. (2021). Interactive wave-structure impacts in aerated water. Technical University Delft; http://resolver.tudelft.nl/uuid:330d9c14-9947-40b0-8fd9-818684da8d56. ; Citation: Eijk & Wellens (2022) Eijk, M. & Wellens, P. (2022). Two-phase free-surface flow interaction with moving bodies with a consistent, momentum preserving method. Journal of Computational Physics. for a complete description of the solving method. Here, I will provide a conceptual explanation of the pressure correction method.

The pressure correction approach consists of what seems a basic iterative procedure between the velocity and the pressure fields (Citation: Hirsch, 2007 Hirsch, C. (2007). Numerical computation of internal and external flows: The fundamentals of computational fluid dynamics (). Elsevier . ) but which turns out to be directly solvable. For an initial approximation of the pressure field, the momentum equation $\cref{eqn:momentum_equation}{2}$ is solved to determine an (intermediate) velocity field $u^*$ containing all explicit terms like convection, diffusion and body forces. The obtained intermediate velocity field does not satisfy the divergence-free property imposed by the continuity equation $\cref{eqn:continuity_equation}{1}$ and should therefore be corrected. Since this velocity correction impacts the pressure field by virtue of the same momentum equation, a related pressure correction should be defined by requiring the corrected velocity to satisfy the continuity equation. The resulting system of equations leads to a Poisson equation for the pressure correction, which can be solved using a linear system solver of choice.

For a full explanation, derivations and implementation details of the pressure correction method, I refer to Citation: Hirsch (2007), pp. 625-637 Hirsch, C. (2007). Numerical computation of internal and external flows: The fundamentals of computational fluid dynamics (). Elsevier . .

Bibliography