Multi-fidelity Kriging extends Kriging to use multiple sources of data with varying levels of accuracy and costs, with the aim to create surrogate model that is more accurate and/or cheaper in terms of the cost of input data.

In this post, I focus on the standard linear auto-regressive formulation of Citation: Gratiet & Garnier (2014) Gratiet, L. & Garnier, J. (2014). Recursive co-kriging model for design of computer experiments with multiple levels of fidelity. International Journal for Uncertainty Quantification, 4(5). 365–386. https://doi.org/10.1615/int.j.uncertaintyquantification.2014006914 in the optimisation context of the EGO adaptive sampling algorithm, and are interested in the potential of this combination to reduce the costs of SBGO. Citation: Meliani, Bartoli & al. (2019) Meliani, M., Bartoli, N., Lefebvre, T., Bouhlel, M., Martins, J. & Morlier, J. (2019). Multi-fidelity efficient global optimization: Methodology and application to airfoil shape design. AIAA Aviation 2019 Forum. https://doi.org/10.2514/6.2019-3236 ; Citation: Korondi, Marchi & al. (2021) Korondi, P., Marchi, M., Parussini, L. & Poloni, C. (2021). Multi-fidelity design optimisation strategy under uncertainty with limited computational budget. Optimization and Engineering, 22(2). 1039–1064. https://doi.org/10.1007/s11081-020-09510-1 use the recursive formulation of Citation: Gratiet & Garnier (2014) Gratiet, L. & Garnier, J. (2014). Recursive co-kriging model for design of computer experiments with multiple levels of fidelity. International Journal for Uncertainty Quantification, 4(5). 365–386. https://doi.org/10.1615/int.j.uncertaintyquantification.2014006914 to introduce a multi-fidelity approach to the EGO algorithm and formulate level-selection criteria that balance the expected reduction of the prediction variance with the costs of sampling a given level. The multi-fidelity SBGO method of Citation: Meliani, Bartoli & al. (2019) Meliani, M., Bartoli, N., Lefebvre, T., Bouhlel, M., Martins, J. & Morlier, J. (2019). Multi-fidelity efficient global optimization: Methodology and application to airfoil shape design. AIAA Aviation 2019 Forum. https://doi.org/10.2514/6.2019-3236 will act as a reference to the method proposed in this thesis since both methods use a so-called nested Design of Experiments (DoE), a sampling strategy that provides the most complete information on the relation between the fidelities (Citation: Kennedy & O’Hagan, 2000 Kennedy, M. & O’Hagan, A. (2000). Predicting the output from a complex computer code when fast approximations are available. Biometrika, 87(1). 1–13. https://doi.org/10.1093/biomet/87.1.1 ).

Citation: Jones (2001) Jones, R. (2001). A Taxonomy of Global Optimization Methods Based on Response Surfaces. Journal of Global Optimization, 21. 345–383. discusses the relation of Kriging with respect to other surrogate modelling methods and explores possible improvements to EGO and the Expected Improvement criterion. As one of the most promising directions for further work, he hinted towards multi-fidelity simulation: using expensive high-precision simulations together with simulations of a lower precision but a much lower cost. This enables us to respectively balance exploitation and exploration of the search space and thereby cut costs while improving the quality of the surrogate.

Since then, Multi-Fidelity Kriging has received significant research effort, see for instance the review papers of Citation: Viana, Simpson & al. (2014) Viana, F., Simpson, T., Balabanov, V. & Toropov, V. (2014). Metamodeling in multidisciplinary design optimization: How far have we really come?. AIAA Journal, 52(4). 670–690. https://doi.org/10.2514/1.J052375 ; Citation: Fernández-Godino, Park & al. (2016) Fernández-Godino, M., Park, C., Kim, N. & Haftka, R. (2016). Review of multi-fidelity models. AIAA Journal, 57(5). 2039–2054. https://doi.org/10.2514/1.J057750 ; Citation: Peherstorfer, Willcox & al. (2018) Peherstorfer, B., Willcox, K. & Gunzburger, M. (2018). Survey of multifidelity methods in uncertainty propagation, inference, and optimization. SIAM Review, 60(3). 550–591. https://doi.org/10.1137/16M1082469 . Citation: Kennedy & O’Hagan (2000) Kennedy, M. & O’Hagan, A. (2000). Predicting the output from a complex computer code when fast approximations are available. Biometrika, 87(1). 1–13. https://doi.org/10.1093/biomet/87.1.1 mathematically formulated the fundamentals, while Citation: Forrester, Sóbester & al. (2007) Forrester, A., Sóbester, A. & Keane, A. (2007). Multi-fidelity optimization via surrogate modelling. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 463(2088). 3251–3269. https://doi.org/10.1098/rspa.2007.1900 provides a more transparent overview. Citation: Gratiet & Garnier (2014) Gratiet, L. & Garnier, J. (2014). Recursive co-kriging model for design of computer experiments with multiple levels of fidelity. International Journal for Uncertainty Quantification, 4(5). 365–386. https://doi.org/10.1615/int.j.uncertaintyquantification.2014006914 show that the model of Citation: Kennedy & O’Hagan (2000) Kennedy, M. & O’Hagan, A. (2000). Predicting the output from a complex computer code when fast approximations are available. Biometrika, 87(1). 1–13. https://doi.org/10.1093/biomet/87.1.1 can be equivalently but more cheaply formulated as recursively nested independent Kriging problems, one for each fidelity level. Citation: Perdikaris, Raissi & al. (2017) Perdikaris, P., Raissi, M., Damianou, A., Lawrence, N. & Karniadakis, G. (2017). Nonlinear information fusion algorithms for data-efficient multi-fidelity modelling. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 473(2198). https://doi.org/10.1098/rspa.2016.0751 improve upon this work by generalising the linear autoregressive¹ formulation of Citation: Gratiet & Garnier (2014) Gratiet, L. & Garnier, J. (2014). Recursive co-kriging model for design of computer experiments with multiple levels of fidelity. International Journal for Uncertainty Quantification, 4(5). 365–386. https://doi.org/10.1615/int.j.uncertaintyquantification.2014006914 to better accommodate non-linear-relations.

Multi-fidelity Kriging

The word ‘fidelity’ can be interpreted as the closeness of a simulation method to the truth. Simulations of a lower fidelity can for instance be obtained by reducing the number of mesh elements, using simpler governing equations, or by letting simulations only partially converge (Citation: Palar, Zuhal & al., 2019 Palar, P., Zuhal, L., Liem, R. & Shimoyama, K. (2019). On the use of surrogate models in engineering design optimization and exploration: The key issues. GECCO 2019 Companion - Proceedings of the 2019 Genetic and Evolutionary Computation Conference Companion. 1592–1602. https://doi.org/10.1145/3319619.3326813 ).

In general, a higher fidelity is more accurate but (much) more expensive than a lower fidelity solution. A multi-fidelity method tries to balance these different costs and accuracies to obtain a result that is more accurate and/or cheaper to obtain than a solution using only the highest fidelity. In the context of the MF-EGO algorithm, it is said we can explore and exploit the objective function using the low- and high-fidelity levels respectively.

Definition

We could describe the relation between two constitutive Kriging levels in a simplified form as (Citation: Forrester, Sóbester & al., 2007 Forrester, A., Sóbester, A. & Keane, A. (2007). Multi-fidelity optimization via surrogate modelling. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 463(2088). 3251–3269. https://doi.org/10.1098/rspa.2007.1900 ):

\begin{equation} Z_{\mathrm{e}}(\boldsymbol{x})=\rho Z_{\mathrm{c}}(\boldsymbol{x})+Z_{\mathrm{d}}(\boldsymbol{x}) \end{equation}

The subscripts respectively indicate ’expensive’, ‘cheap’, and ‘difference’. $\rho$ is a constant multiplicative scaling parameter. The difference model can be regarded as a surrogate model itself.

The auto-regressive method of Citation: Kennedy & O’Hagan (2000) Kennedy, M. & O’Hagan, A. (2000). Predicting the output from a complex computer code when fast approximations are available. Biometrika, 87(1). 1–13. https://doi.org/10.1093/biomet/87.1.1 can equivalently be recursively formulated to solve the problem at a much-reduced cost (Citation: Gratiet & Garnier, 2014 Gratiet, L. & Garnier, J. (2014). Recursive co-kriging model for design of computer experiments with multiple levels of fidelity. International Journal for Uncertainty Quantification, 4(5). 365–386. https://doi.org/10.1615/int.j.uncertaintyquantification.2014006914 ). The recursive formulation of the Kriging predictor and MSE estimate then becomes:

The effectiveness of this multi-fidelity formulation is typically exemplified using the somewhat contrived example of Citation: Forrester, Sóbester & al. (2007) Forrester, A., Sóbester, A. & Keane, A. (2007). Multi-fidelity optimization via surrogate modelling. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 463(2088). 3251–3269. https://doi.org/10.1098/rspa.2007.1900 :

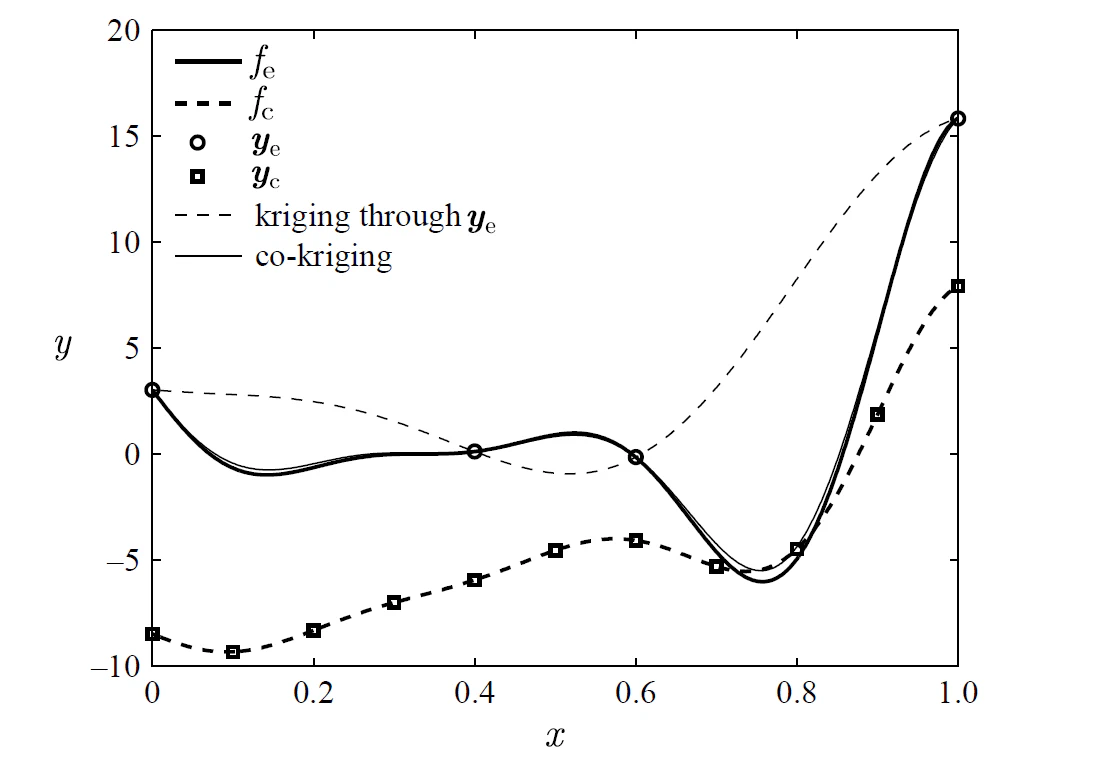
Usage conditions

The implicit presumption of multi-fidelity Kriging is that the difference model $Z_{\mathrm{d}}(\boldsymbol{x})$ is simpler and thus easier to predict than the true response surface. For this to be true we require a high correlation between the fidelity levels. Citation: Toal (2015) Toal, D. (2015). Some considerations regarding the use of multi-fidelity Kriging in the construction of surrogate models. Structural and Multidisciplinary Optimization, 51(6). 1223–1245. https://doi.org/10.1007/s00158-014-1209-5 provides an indication of the conditions in which bi-fidelity Kriging is more efficient or effective than single-fidelity Kriging:

• The correlation between the low and high fidelity function should be reasonably high, $r^2 > 0.9$
• More than 10 % but no more than 80% of the total evaluation budget should be converted to cheap evaluations, $0.1 < f_r < 0.8$.
• There should always be slightly more cheap data points than expensive with the inequality, $f_r > \frac{1.75}{1+\frac{1}{C_r}}$, giving a conservative bound for this condition

Here $f_r$ denotes the fraction of the number of expensive evaluations over the number of cheap evaluations and similarly, $C_r$ denotes the ratio of simulation costs. Although these criteria might not always be accurate, they at least provide some intuition to the practical use of multi-fidelity Kriging.

Bibliography